一般選抜で受験をする人は多かれ少なかれ,模試の判定を気にするでしょう。
判定はAからEまであると思いますが,なんとなくAが良い判定で,Eが悪い判定としか思っていない人も多いでしょう。
今回は大学受験の判定とはいったい何ぞやということを書いていこうと思います。

自己紹介
そもそもA判定~E判定は何?
ざっくりと説明すると,それぞれの合格可能性はこんな感じです。
- A判定 80%以上
- B判定 60%~80%
- C判定 40%~60%
- D判定 20%~40%
- E判定 20%未満
そもそも合格可能性とは?
ということはA判定の人は10回受けたら,8回受かるということ?そんなに受験しないでしょ,と思うかもしれません。
そんなに受験することはないですね。
A判定とは,例えば過去にある成績の人が10人いたとして,8人が合格しました,という意味です。
模試は何万人という人が受験します。
当然,同じ偏差値の人が,同じ大学・学部・学科・入試方式を受験することはあります。
受験が終わると受験生宛てに受験結果を報告してくれるとプレゼントがもらえることがあります。
大手予備校はこの受験結果報告で,どの模試で,どの点数を取った人が,どこに・どんな方式で受かったか,あるいは落ちたかデータベースを作成します。
そのデータベースを次年度以降の模試で判定を出すのに使うのです。
分かりやすく架空の例を示したいと思います。
高校3年10月実施の模試を受験した人の中で,その後●●大学▲▲学部★★学科の■■方式を受験した人を抽出してデータベースを作ったとします。
(表が細かくなるので,偏差値は2ポイントきざみにしました)
| 偏差値 | 合格者数 | 不合格者数 | 受験者数計 | 合格可能性 | 判定 |
| 66 | 5 | 0 | 5 | 100% | A |
| 64 | 10 | 2 | 12 | 83% | A |
| 62 | 15 | 5 | 20 | 75% | B |
| 60 | 20 | 15 | 35 | 57% | C |
| 58 | 15 | 20 | 35 | 43% | C |
| 56 | 10 | 25 | 35 | 29% | D |
| 54 | 5 | 23 | 28 | 18% | E |
| 52 | 3 | 20 | 23 | 13% | E |
| 50 | 1 | 16 | 17 | 6% | E |
偏差値の高い層に合格者数が多く,低い層に不合格者数が固まっているのが見て取れます。
大学が行う入試本番の合否は定員を基に特定の点数をボーダーラインにします。
完全に同じ点数で合格者と不合格者が出ることはありません。
(完全にというのは大学によって調査書等を点数化する場合もあるので,そういった計算も含めた点数という意味です)
模試を受けてから入試本番までは時間があるので,人により学力が伸びたり,伸び悩んだりすることはあるでしょう。
模試の時は同じ偏差値でも入試の点数で差が付き合否が分かれます。
このように受験者数と合格者数の割合で合格可能性や合否判定を出していきます。
よく「E判定でもあきらめるな」と元気づける人がいます。
この表を見れば,まったく希望がないわけではありませんが,E判定だけの大学で受験校を固めるのはかなり厳しい受験になることがわかるでしょう。

ドラマ「二月の勝者」では模試の過去問を演習するシーンがありました。
ドラマで触れられたメリット以外にも,大問の数,問いの種類(英語の場合,文法問題の量,長文問題の量など),問われ方(記述,マークなど)を把握しておくことは高得点に近づきます。
テストというのはその教科の力だけを正確に測ることができません。
問題数,問いの種類,問われ方によって,同じ分野であって正答率は異なります。
そこで本番に向けて過去問を演習するのと同様に,模試にも準備をして臨んだ方が高得点につながりますし,一番努力が点数に表れやすいのです。
大手予備校の大学受験の模試の場合,マーク模試は共通テストを想定して,記述模試は二次試験や個別試験を想定して実施されます。
なのでほとんどの高3生の受験生はすでに触れたことのある出題形式です。
模試の過去問演習はあまり問題演習に時間を避けていない高2生までの学年で積極的に取り入れるのがいいでしょう。
模試によって判定がずれるのはなぜ?
ただ,模試によって判定がずることがあります。
こんな要因が考えられます。
本人の調子が良かったor悪かった
模試はあくまでその時の点数でデータ処理をします。
人間なので体調不良,問題との相性などで,調子が良し悪しが変わることがあるでしょう。
それら要因により点数が振るわなかったということはありえます。
ただ,この場合は偏差値も下がるので判定が下がった場合,本人も原因がわかるでしょう。
模試を実施した予備校が独自の分析をしている
大手予備校等は何年にもわたって受験生のデータが蓄積しています。
また大学を取り巻く環境の変化なども分析しています。
- キャンパス移転(交通の便の良し悪し)
- 定員の増減
- 近年のその大学(・学部・学科)の人気・不人気
- 学問系統の人気・不人気
- 近年の受験生の志望者数を増減
など
こういったものを加味して,少し判定を厳しくしたり,緩めたり?することもあると聞いたことがあります。
模試によって受験生の学力層や受験者数が変わる
大学受験生の多くが受験するタイプの模試か,高い成績層の受験生が主に受験するタイプの模試かによって判定が変わることがあります。
特に、例えばGMARCH志望者を対象にした模試は要注意!
最難関国公立、早慶のライバルは、その大学を受験する人だけです。
しかし、GMARCHレベルを受験する人のライバルは、
の両方がライバルです。
そして、GMARCH志望者に絞った模試を、GMARCHを第二志望以下にしている人は受けないことも多いです。
だって、模試を受けなくても合格できそうだから。
そうなると、データの正確性が欠けるので、判定に揺らぎが出てきやすいと言えます。
志望校として書いていない受験生が後で受験を考える場合がある
合格可能性判定は20%刻みになっているので,影響がどの程度かはケースバーケースです。
思ったより志望校に登録した受験生が多く,倍率が上がることを懸念して急に嫌煙されるかもしれません。
そうなると,厳しい判定であった受験生が合格を勝ち取ることもあるかもしれません。
また、逆も起こりえます。
A判定でも不合格になり,E判定でも合格になる理由
模試と本番では出題形式が異なります。
英語の場合,英作文の有無や形式,リスニングの有無,長文の長さなど細かいことをあげたらきりがありません。
自分の得意な問われ方の場合,高得点が期待できるかもしれません。
共通テストであっても,馴染み深い話題かどうかが得点に影響を与えます。
大学受験は人数が多いので,1点違えば数十人,受験形式によっては数百人を追い抜かしたり,追い抜かれたりします。
難関大学など志願者の成績分布が高得点帯に集中している場合,募集人数が少ない場合,数点刻みでA〜D判定の幅が狭いことがあります。
その場合は逆転も起きるかもしれません。
下の図で右に行けば好成績,上に行けば人数が多いということになります。
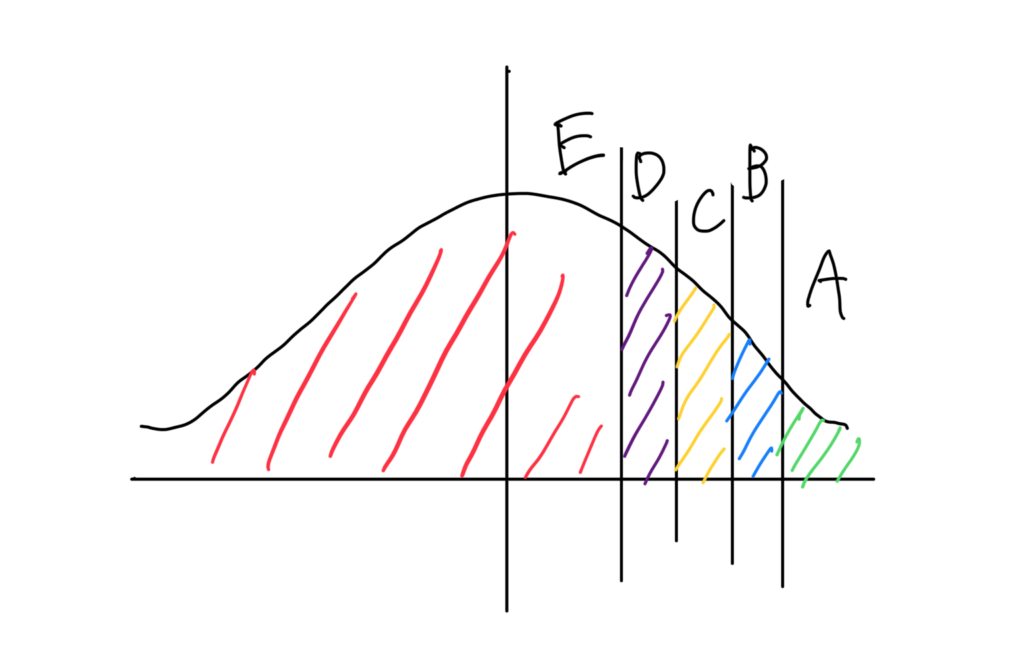
東大,早慶など最難関の大学は高得点に受験生が集中しますし,さらに人数枠が狭いと,こんな感じになります。
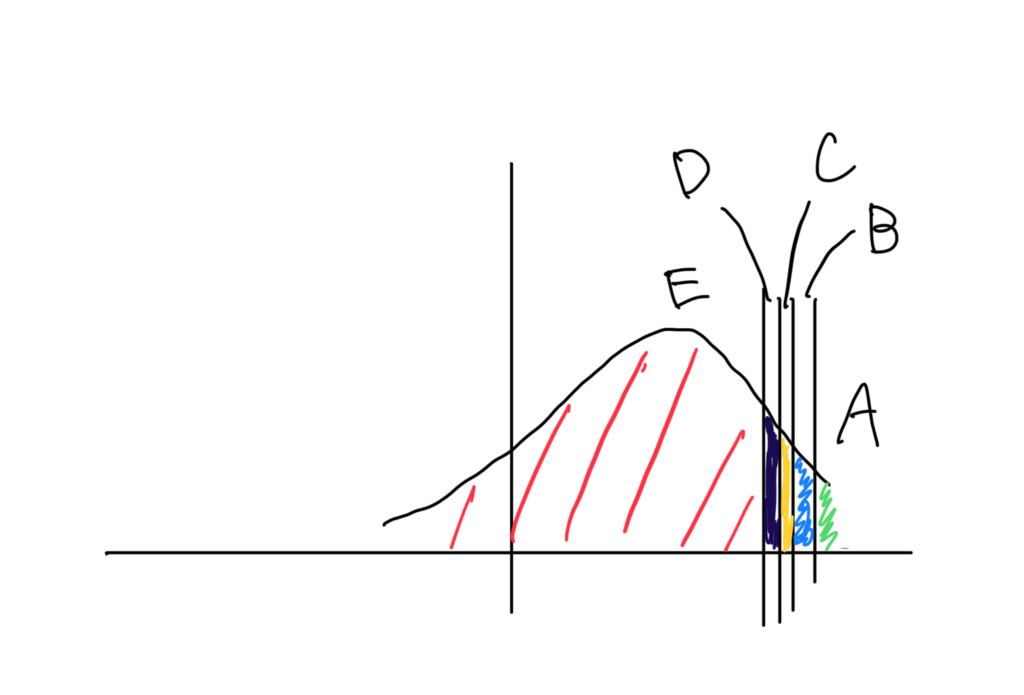
同じE判定でも、惜しいE判定と、道が険しいE判定があります。
D判定の境目にいる人は、意外にC判定、B判定まで1科目あたり10点未満の位置にいることがあります。
問題数にすると、全科目あと2~3問ずつ正解すればC判定に到達できることもあります。
一方、E判定には底がありませんので、なかなか道が険しいこともあります。
模試の結果が帰ってきたら、たとえE判定でも、E判定の中でどの位置にいるか確認しよう!
受験計画,志望校の決め方
受験計画は人それぞれですが,浪人を避ける前提で一般的なものを紹介します。
- 第一志望 1校
- B判定〜C判定の大学・学部・学科・入試方式 2〜3校
- A判定の大学・学部・学科・入試方式 1校
大学受験は大学・学部・学科・入試方式により異なりますので,第一志望の大学・学部・学科・入試方式に合わせるのが良いです。
わざわざ滑り止めのために1科目多く勉強するのは厳しいでしょう。
もちろん,大学へのこだわりや受験料を負担できるかどうかなどによっても変わってきます。
模試を受験していれば,過去のデータをもとに予備校や受験指導の環境が整った学校の先生なら滑り止めの候補を提示することができると思います。
第一志望校は高2の秋ごろまでには決めておき,目標に向かって頑張りましょう。
滑り止めは高3の秋くらいに固められるといいですね。
入学手続き日にも注意!
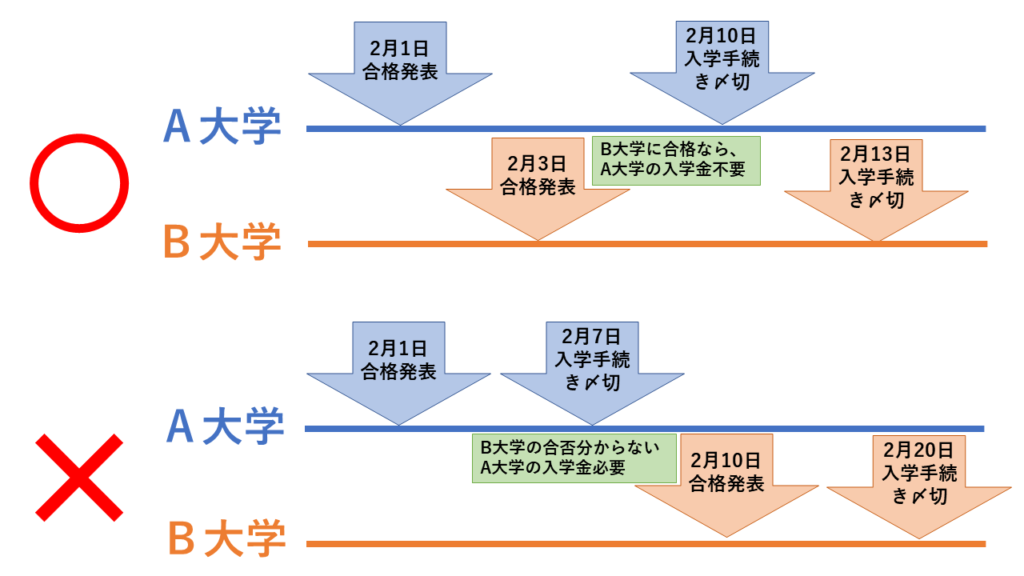
複数の大学を受けるとき、受験日、合格発表日、入学手続き締切日がずれます。
合格発表日と入学手続き日を上手にずらしながら計画したいですね。
2/1 A大学 合格発表
2/3 B大学 合格発表
2/10 A大学 入学手続き締切日
2/13 B大学 入学手続き締切日
このパターンなら、A大学、B大学の両方に合格した場合、A大学の入学金を振り込まずに済みます。
2/1 A大学 合格発表
2/7 A大学 入学手続き締切日
2/10 B大学 合格発表
2/20 B大学 入学手続き締切日
このパターンになると、C大学の入学金を払わないと、D大学が不合格なら、合格の権利を失ってしまいます。
まとめ
いかがでしたでしょうか。
今まではなんとなく理解していたつもりの模試の判定ですが,少しクリアになってきたのではないでしょうか。
受験生のみなさんは,希望を捨てず,ただうぬぼれることなく勉強を頑張ってください!
ちなみに試験問題の作り方についてここで少し触れました。















コメント